Mengenal t-SNE: Teknik Visualisasi untuk Menggali Pola Tersembunyi dalam Data

Di dunia yang semakin digital ini, data menjadi elemen penting dalam hampir setiap aspek kehidupan kita. Namun, mengolah dan memahami data yang kompleks dan berdimensi tinggi dapat menjadi tantangan tersendiri. Misalnya, dalam bidang kesehatan, para peneliti sering kali bekerja dengan dataset besar yang berisi ribuan gen untuk menemukan pola genetik yang dapat mengindikasikan penyakit tertentu. Demikian pula, di industri teknologi, perusahaan menggunakan data perilaku pengguna untuk mempersonalisasi pengalaman dan merekomendasikan produk yang tepat. Sementara itu, di bidang keuangan, analisis data yang akurat dapat membantu mendeteksi aktivitas penipuan dan tren pasar.

Di tengah-tengah kompleksitas ini, salah satu teknik yang dapat membantu kita adalah t-distributed Stochastic Neighbor Embedding atau yang lebih dikenal dengan t-SNE. t-SNE adalah teknik visualisasi yang mampu mengubah data berdimensi tinggi menjadi representasi dua atau tiga dimensi yang lebih mudah dipahami. Dengan t-SNE, para analis dan peneliti dapat menggali pola tersembunyi dalam data, menemukan kluster yang tidak terduga, dan mengidentifikasi anomali yang mungkin terlewatkan oleh metode reduksi dimensi data lainnya. Artikel ini akan mengupas lebih dalam tentang t-SNE, membahas cara kerjanya, perbedaan dengan teknik lain seperti PCA, serta manfaat dan kekurangannya.

Apa itu t-SNE

t-SNE adalah teknik untuk membantu kita memahami dan memvisualisasikan data yang memiliki dimensi tinggi dengan cara yang lebih intuitif. Dalam istilah yang lebih sederhana, t-SNE memungkinkan kita untuk melihat data yang kompleks dalam bentuk yang lebih sederhana, seperti grafik dua atau tiga dimensi. Teknik ini sangat berguna untuk menggali pola tersembunyi dalam data yang tidak dapat dengan mudah dilihat dengan metode visualisasi tradisional.

t-SNE bekerja dengan cara mengubah jarak antara titik data dalam ruang dimensi tinggi, misalnya dataset yang memiliki fitur yang sangat banyak. Lalu, mengubah setiap jarak antar data menjadi peluang, yang menggambarkan seberapa besar kemungkinan dua titik adalah tetangga dekat. Dengan melakukan ini, t-SNE menjaga struktur lokal dari data sehingga pola atau kelompok yang mirip tetap terlihat jelas dalam representasi dimensi rendah. Struktur lokal disini maksudnya adalah tertangga terdekat, selain struktur lokal ada juga struktur global yang berarti relasi antar kluster data. Inilah yang membuat t-SNE menjadi alat yang sangat efektif dalam memvisualisasikan dan memahami data yang kompleks, seperti gambar, suara, atau data genetik.

Mengapa t-SNE Dibutuhkan

Dalam dunia analisis data, kita sering kali dihadapkan pada tantangan untuk menemukan pola atau kluster dalam data yang tidak terstruktur. Misalnya, data yang dihasilkan oleh sensor canggih atau gambar digital sering kali memiliki ratusan hingga ribuan variabel. Visualisasi dengan teknik biasa seperti grafik atau tabel tidak dapat mengungkapkan hubungan yang mendalam di antara variabel-variabel ini. t-SNE menjadi solusi karena dapat memberikan gambaran yang lebih jelas dan detail tentang bagaimana data tersebut berinteraksi satu sama lain.

Selain itu, t-SNE dapat membantu dalam berbagai aplikasi praktis. Dalam industri kesehatan, misalnya, t-SNE dapat digunakan untuk menganalisis data genetik untuk menemukan pola yang mengindikasikan penyakit. Di bidang pemasaran, perusahaan dapat menggunakan t-SNE untuk menganalisis perilaku konsumen dan mengelompokkan pengguna berdasarkan preferensi mereka. Dengan kata lain, t-SNE tidak hanya membantu kita memahami data yang rumit tetapi juga membuka peluang baru untuk menemukan wawasan yang berharga.

Apa Perbedaannya Dengan PCA

Principal Component Analysis (PCA) adalah teknik reduksi dimensi lain yang sering digunakan dalam analisis data. Meskipun PCA juga dapat membantu dalam mereduksi dimensi data, ada beberapa perbedaan mendasar antara PCA dan t-SNE:

• Fokus pada Struktur: PCA lebih berfokus pada menjaga variasi global dalam data, sedangkan t-SNE lebih menitikberatkan pada menjaga struktur lokal. Ini berarti t-SNE lebih baik dalam menangkap pola atau kluster kecil yang mungkin diabaikan oleh PCA.

• Metode Reduksi Dimensi: PCA menggunakan transformasi linear untuk mereduksi dimensi data, yang berarti ia meratakan data ke dalam ruang dengan lebih sedikit dimensi. Sebaliknya, t-SNE menggunakan pendekatan non-linear, yang lebih fleksibel dalam menangkap hubungan kompleks antar data.

• Visualisasi Kluster: Dalam hal visualisasi kluster, t-SNE cenderung memberikan gambaran yang lebih jelas dan terpisah tentang kluster dalam data, sedangkan PCA mungkin tidak selalu menghasilkan visualisasi yang memisahkan kluster dengan baik.

Kapan Menggunakan PCA dan t-SNE

Ketika berhadapan dengan data berdimensi tinggi, baik t-SNE maupun PCA bisa menjadi pilihan untuk mereduksi dimensi dan memvisualisasikan data. Namun, masing-masing teknik memiliki keunggulan dan batasannya sendiri, tergantung pada situasi dan tujuan analisis. PCA adalah teknik yang sangat berguna ketika tujuan utamanya adalah memahami variasi terbesar dalam data. Ia bekerja dengan mengubah data ke dalam ruang dimensi yang lebih rendah melalui transformasi linear, mempertahankan sebanyak mungkin variasi total dari data asli. PCA sering digunakan ketika dataset besar dan berisi noise, serta ketika kita ingin menjaga struktur global data untuk analisis lebih lanjut, seperti regresi atau pengelompokan.

Sebaliknya, t-SNE lebih unggul ketika fokusnya adalah pada eksplorasi dan visualisasi pola lokal yang rumit dalam data. Ia sangat efektif untuk memvisualisasikan data non-linear dan data yang memiliki kluster kompleks, seperti gambar atau data genetik, di mana hubungan antar data tidak dapat dijelaskan dengan baik oleh metode linear. Teknik ini sangat berguna ketika kita ingin melihat bagaimana data mengelompok secara alami, menemukan pola tersembunyi, atau mengidentifikasi subkluster dalam data yang mungkin diabaikan oleh PCA.

Dalam praktiknya, t-SNE sering dipilih ketika tujuan utamanya adalah visualisasi data untuk presentasi atau eksplorasi awal dataset yang sangat kompleks. Sebagai contoh, dalam analisis gambar, t-SNE dapat digunakan untuk melihat bagaimana gambar-gambar serupa terkelompok secara visual. Namun, perlu diingat bahwa t-SNE tidak selalu ideal untuk semua situasi, terutama jika kecepatan dan efisiensi komputasi menjadi prioritas, mengingat t-SNE bisa lebih lambat dan memerlukan lebih banyak sumber daya dibandingkan PCA. Memilih antara t-SNE dan PCA sering kali bergantung pada jenis data yang kita miliki dan apa yang ingin kita capai dengan analisis tersebut.

Cara Kerja t-SNE

Sekarang kita akan memahami cara kerja t-SNE, bagi menjadi beberapa langkah penting.

1. Menghitung Jarak Lokal Langkah pertama dalam t-SNE adalah mengukur seberapa mirip dua titik data dalam dimensi yang lebih tinggi. Bayangkan kamu memiliki banyak titik yang tersebar di ruang tiga dimensi, seperti bintang di langit. Untuk setiap pasangan titik, t-SNE menghitung jarak antara mereka menggunakan rumus jarak Euclidean, yaitu: 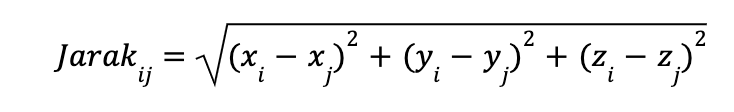Dimana xi, yi, zi adalah koordinat titik i, dan xj, yj, zj adalah koordinat titik j. Jarak ini membantu t-SNE memahami seberapa dekat atau jauh titik-titik tersebut satu sama lain.

2. Memetakan ke Peluang Setelah menghitung jarak, t-SNE mengubah jarak ini menjadi probabilitas, yaitu kemungkinan bahwa titik-titik tersebut adalah tetangga dekat. Ini mirip dengan menghitung seberapa mungkin seseorang berteman dengan orang lain berdasarkan seberapa dekat mereka tinggal. Rumus yang digunakan adalah:

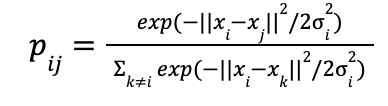
Di sini, pij adalah probabilitas bahwa titik i dan j adalah tetangga, dan adalah parameter yang menentukan seberapa luas lingkungan yang dipertimbangkan untuk titik i. Nilai i diatur untuk menentukan jumlah tetangga lokal, atau disebut perplexity.

3. Pengurangan Dimensi Setelah mendapatkan peluang di dimensi tinggi, t-SNE mencoba memetakan titik-titik tersebut ke dalam ruang dimensi rendah, seperti 2D atau 3D, dengan menjaga probabilitas yang sama antara titik. Ini berarti t-SNE akan menyesuaikan posisi titik di ruang 2D/3D sehingga hubungan antar titik tetap konsisten dengan yang ada di dimensi tinggi.

4. Optimasi Langkah terakhir adalah menyesuaikan posisi titik-titik dalam ruang dimensi rendah agar distribusi probabilitas antara titik dalam ruang ini sedekat mungkin dengan distribusi probabilitas di dimensi tinggi. Untuk melakukan ini, t-SNE menggunakan algoritma optimasi yang disebut gradient descent, yang bertujuan meminimalkan perbedaan antara dua distribusi probabilitas tersebut. Proses ini bisa dianalogikan seperti mencoba menyesuaikan posisi benda-benda di meja agar terlihat sama persis dengan foto aslinya.

Kelebihan dan Kekurangan t-SNE

t-SNE adalah alat yang luar biasa untuk memvisualisasikan data yang rumit, tetapi seperti alat lainnya, ia memiliki kelebihan dan kekurangannya sendiri. Mari kita bahas satu per satu.

Kelebihan t-SNE:

1. Menangkap Struktur Lokal dengan Baik: Salah satu keunggulan terbesar t-SNE adalah kemampuannya untuk menangkap struktur lokal dalam data. Ini berarti t-SNE sangat bagus dalam menemukan pola kecil atau kluster data yang mungkin terlewatkan oleh metode lain. Misalnya, jika kita memiliki dataset gambar yang mirip tetapi memiliki perbedaan kecil, t-SNE dapat membantu kita melihat perbedaan tersebut dengan lebih jelas.

2. Memudahkan Visualisasi Data Kompleks: t-SNE dirancang untuk mereduksi dimensi data yang sangat tinggi menjadi dua atau tiga dimensi yang lebih mudah dipahami. Hal ini sangat berguna ketika kita ingin melihat data yang memiliki ratusan atau ribuan fitur. Dengan t-SNE, kita bisa mendapatkan gambaran yang lebih sederhana tentang bagaimana data tersebut dikelompokkan atau tersebar.

Kekurangan t-SNE

1. Komputasi Intensif untuk Dataset Besar: t-SNE bisa menjadi sangat lambat ketika diterapkan pada dataset yang sangat besar. Proses perhitungan jarak antar semua pasangan titik dan optimasi posisi dalam ruang rendah memerlukan banyak sumber daya komputasi. Ini bisa menjadi masalah jika kita ingin menganalisis dataset dengan jutaan titik data.

2. Tidak Selalu Menjaga Struktur Global: Sementara t-SNE hebat dalam menangkap struktur lokal, ia kadang-kadang mengorbankan struktur global dari data. Ini berarti bahwa hubungan antara kluster besar atau pola global dalam data mungkin tidak selalu terlihat jelas dalam hasil visualisasi t-SNE. Jadi, jika kita tertarik pada hubungan global antar kluster, kita harus berhati-hati dalam menginterpretasikan hasil t-SNE.

3. Sensitif terhadap Parameter seperti Perplexity: t-SNE memiliki beberapa parameter yang perlu diatur dengan hati-hati, salah satunya adalah perplexity. Nilai perplexity yang dipilih dapat secara signifikan mempengaruhi hasil visualisasi. Jika nilainya terlalu rendah atau terlalu tinggi, visualisasi mungkin tidak menggambarkan data dengan benar. Oleh karena itu, eksperimen dengan berbagai nilai parameter sering kali diperlukan untuk mendapatkan hasil terbaik.

Parameter dalam t-SNE dan Fungsinya

Ketika kita menggunakan t-SNE untuk memvisualisasikan data, ada beberapa pengaturan penting yang perlu kita atur agar hasilnya sesuai dengan yang kita harapkan. Ini disebut parameter. Mari kita lihat parameter-parameter utama dalam t-SNE dan apa fungsinya.

1. Perplexity menentukan seberapa banyak tetangga yang akan diperhitungkan saat menentukan posisi titik-titik data. Jika kita memilih nilai perplexity yang lebih tinggi, t-SNE akan mempertimbangkan lebih banyak titik sebagai tetangga. Perplexity biasanya berkisar antara 5 hingga 50. Jika terlalu rendah, kita mungkin kehilangan gambar besar, dan jika terlalu tinggi, kita mungkin kehilangan detail kecil.
2. Learning rate adalah seberapa cepat atau lambat t-SNE belajar dari data untuk menyesuaikan posisi titik-titiknya. Jika kita memilih nilai learning rate yang terlalu rendah, t-SNE mungkin terlalu lambat dalam menemukan posisi terbaik untuk setiap titik. Sebaliknya, jika terlalu tinggi, titik-titik mungkin bergerak terlalu cepat dan bisa melewatkan posisi yang tepat. Jadi, learning rate membantu mengontrol kecepatan belajar t-SNE.
3. Jumlah iterasi adalah berapa kali t-SNE akan mencoba menyesuaikan posisi titik-titik data. Semakin banyak iterasi yang kita lakukan, semakin baik t-SNE dapat menyesuaikan titik-titiknya. Pikirkan iterasi seperti berapa banyak langkah yang kita ambil untuk menyusun puzzle. Semakin banyak langkah, semakin dekat kita dengan gambaran akhir. Namun, terlalu banyak iterasi juga bisa menghabiskan waktu dan sumber daya, jadi kita perlu menemukan jumlah yang tepat.
4. Komponen adalah berapa banyak dimensi akhir yang kita inginkan untuk data kita. Biasanya, kita ingin data kita dalam bentuk dua atau tiga dimensi, sehingga kita bisa melihatnya dengan mudah di layar atau di kertas. Memilih jumlah komponen yang tepat membantu kita mendapatkan visualisasi yang jelas dan mudah dipahami.

Sekarang setelah kita memahami konsep dasar t-SNE dan bagaimana teknik ini dapat membantu dalam mereduksi dimensi data yang kompleks, saatnya kita melihat penerapannya dalam dunia nyata. Dalam bagian ini, kita akan menggunakan bahasa pemrograman Python untuk menerapkan t-SNE dengan contoh sederhana yaitu menggunakan dataset Iris. Dataset ini berisi informasi tentang tiga spesies bunga iris dan memiliki empat fitur: panjang sepal, lebar sepal, panjang petal, dan lebar petal. Dengan bantuan t-SNE, kita akan memvisualisasikan bagaimana spesies-spesies ini dikelompokkan berdasarkan fitur mereka dalam ruang dua dimensi. Proses ini akan memberi kita wawasan tentang bagaimana pola dan kluster dalam data Iris dapat diidentifikasi dan dipahami dengan lebih mudah.

Menggunakan t-SNE untuk Memahami Pola dalam Dataset Iris dengan Python

Kita menggunakan beberapa library Python yang populer untuk analisis data dan visualisasi: numpy, matplotlib, seaborn, dan sklearn.

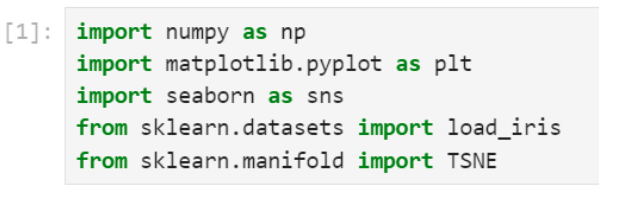Gambar 1. Impor library yang diperlukan

Kita menggunakan dataset yang tersedia dari libary sklearn, lihat gambar 2 untuk bagaimana cara load datasetnya. Kita langsung bagi dataset menjadi fitur berisi ukuran sepal dan petal, kemudian simpan ke variabel X. Lalu target berisi label kelas atau spesies bunga, kita simpan ke dalam variabel y.

Gambar 2. Menyiapkan data

Kita akan menerapkan t-SNE untuk mereduksi data berdimensi tinggi (4D) menjadi 2D agar mudah divisualisasikan.

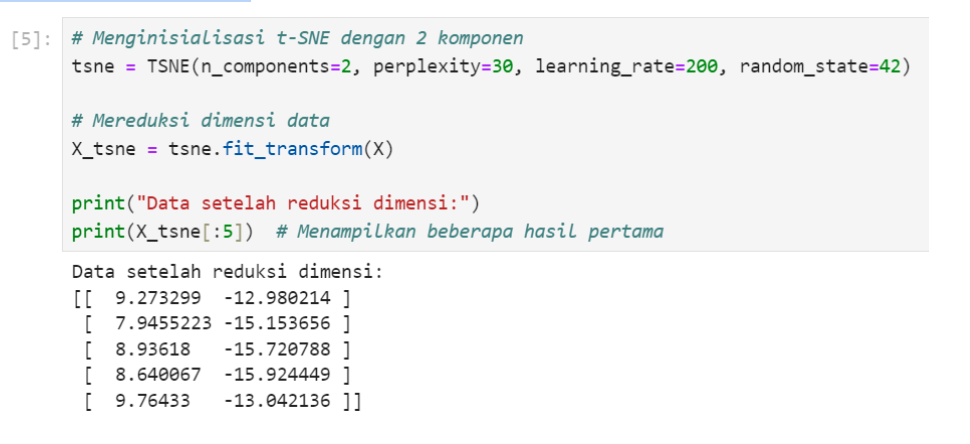Gambar 3. Menerapkan t-SNE ke fitur

Pada gambar 3 kita menyetel parameter yaitu n_components=2 menentukan jumlah dimensi yang diinginkan dalam hasil akhir, dalam hal ini 2D. perplexity=30 menentukan berapa banyak tetangga yang akan dipertimbangkan saat mereduksi dimensi. learning_rate=200 mengatur kecepatan belajar algoritma t-SNE. random_state=42 mengatur seed untuk mendapatkan hasil yang dapat direproduksi.

Setelah mendapatkan hasil dari t-SNE, kita akan memvisualisasikannya menggunakan scatterplot seperti yang ditunjukkan pada gambar 4.

Gambar 4. Menampilkan hasilnya ke visualisasi scatterplot

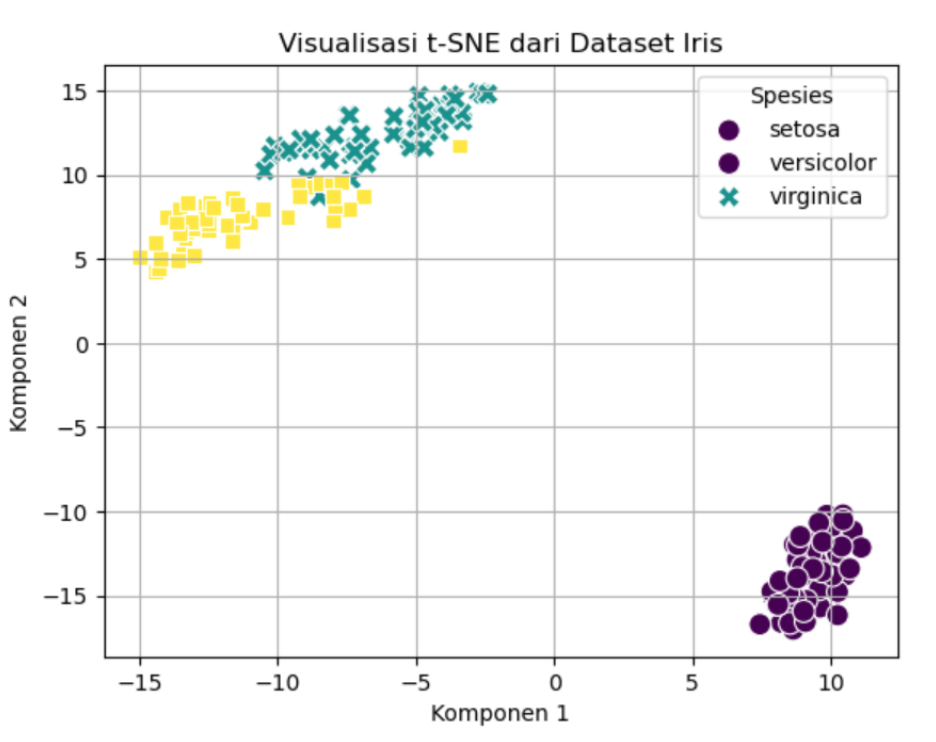Gambar 5. Visualisasi scatterplot hasil pengelompokan t-SNE

Dapat dilihat gambar 5 menunjukkan komponen 1 dan komponen 2, dua dimensi yang dihasilkan oleh t-SNE, merepresentasikan hubungan antara titik data berdasarkan fitur aslinya. Kita juga dapat melihat kluster yang dikumpulkan oleh t-SNE membagi setiap spesies bunga, sehingga kita bisa melihat perbedaan dan kesamaan di antara spesies.

t-SNE adalah teknik yang sangat berguna dalam dunia analisis data, terutama ketika kita berhadapan dengan data yang kompleks dan berdimensi tinggi. Dengan kemampuannya untuk mengubah data tersebut menjadi visualisasi dua atau tiga dimensi, t-SNE membantu kita untuk menemukan pola tersembunyi, mengidentifikasi kluster, dan menggali wawasan baru yang mungkin terlewatkan oleh teknik lain. Salah satu manfaat utama t-SNE adalah kemampuannya untuk menangkap struktur lokal dengan baik, yang sangat penting ketika kita ingin memahami hubungan dalam data yang tidak linier.

Namun, seperti teknik lainnya, t-SNE juga memiliki keterbatasan. Misalnya, ia bisa sangat intensif secara komputasi ketika diterapkan pada dataset yang sangat besar, dan hasil visualisasinya bisa sensitif terhadap parameter seperti perplexity dan learning rate. Oleh karena itu, penting untuk memilih parameter yang tepat dan bereksperimen dengan data untuk mendapatkan hasil yang optimal. Selain itu, pengguna juga harus memahami bahwa t-SNE mungkin tidak selalu menjaga struktur global dari data, sehingga interpretasi hasil visualisasi harus dilakukan dengan hati-hati.

Secara keseluruhan, t-SNE adalah alat yang kuat untuk memvisualisasikan dan memahami data yang rumit. Dengan memilih teknik dan parameter yang tepat, t-SNE dapat menjadi jembatan yang menghubungkan data yang kompleks dengan wawasan yang bermanfaat.