Dari Teorema Bayes ke Aplikasi Dunia Nyata: Memahami Klasifikasi Naive Bayes

Supervised Learning merupakan salah satu pilar utama dalam machine learning yang membantu memberikan prediksi yang tepat. Terutama, klasifikasi melakukan prediksi berdasarkan fitur-fitur tertentu. Naive Bayes adalah salah satu metode klasifikasi yang cukup populer karena sederhana dan peran efektivitasnya dalam beberapa penerapannya pada dunia nyata, seperti email spam detection, weather prediction, medical diagnosis, text classification, dan recommendation system. Artikel ini secara khusus akan membahas terkait Naive Bayes dari dasar hingga penerapan praktis. Untuk info lebih lanjut, baca terus sampai akhir dan nikmati prosesnya!

Permulaan tentang Naive Bayes

Mari kita jelajahi algoritma Naive Bayes, sebuah teknik klasifikasi yang berdasarkan pada Teorema Bayes dengan asumsi bahwa semua fitur yang memprediksi nilai target adalah independen satu sama lain. Algoritma ini menghitung probabilitas setiap kelas dan kemudian memilih yang memiliki probabilitas tertinggi. Algoritma ini berasal dari karya Thomas Bayes dan prinsip-prinsip Bayesian, terutama probabilitas kondisional. "Naive" di sini berarti asumsi bahwa fitur-fitur bersifat independen dan tidak berpengaruh terhadap satu sama lain. Untuk memahami cara kerja Naive Bayes, kita akan melihat penerapannya dalam kehidupan nyata. Misalnya, kita akan menggunakan contoh sederhana: email spam detection. Melalui ilustrasi ini, kita akan memahami proses langkah demi langkah bagaimana Naive Bayes menghitung probabilitas dan menggunakan Teorema Bayes untuk klasifikasi. Siap untuk memulai? Yuk, lanjut baca dan kita telusuri bersama!

1. Teorema Bayes Teorema Bayes, yang ditemukan oleh Thomas Bayes, adalah dasar dari algoritma Naive Bayes. Teorema ini membantu kita dalam proses **menghitung probabilitas **suatu peristiwa berdasarkan informasi yang sudah kita ketahui sebelumnya. Secara sederhana, Teorema Bayes menyatakan bahwa kita bisa memperbarui keyakinan kita tentang suatu peristiwa dengan menggunakan bukti baru. Secara matematis, Teorema Bayes ditulis sebagai: 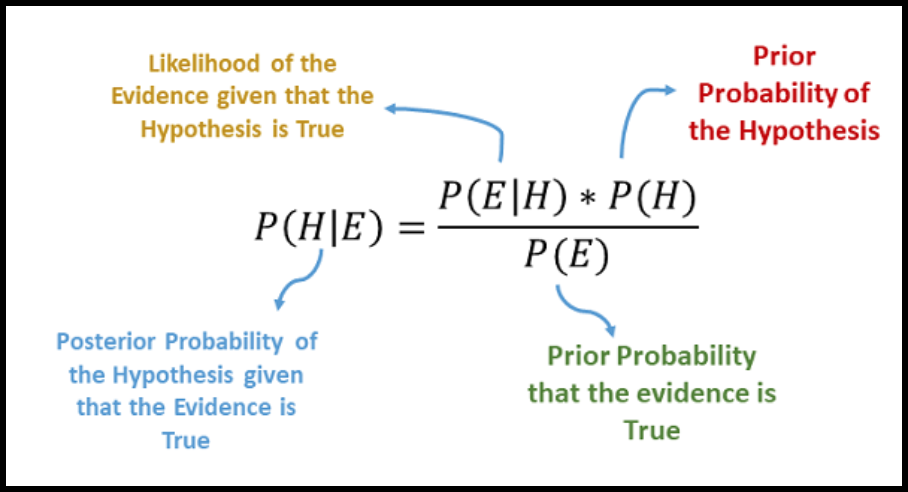Gambar 1. Persamaan matematika teorema bayes

Di sini, P(H∣E) adalah probabilitas H terjadi diberikan E, P(E∣H) adalah probabilitas E terjadi diberikan H, P(H) adalah probabilitas H terjadi, dan P(E) adalah probabilitas E terjadi. Dalam konteks deteksi email spam, kita bisa menggunakan teorema ini untuk menghitung probabilitas sebuah email merupakan spam berdasarkan kata-kata yang ada di dalamnya. Misalnya, kita ingin mengetahui apakah email dengan kata "gratis" adalah spam atau bukan. Dengan Teorema Bayes, kita bisa menghitung probabilitas email itu adalah spam jika mengandung kata "gratis" dengan melihat seberapa sering kata "gratis" muncul di email spam dibandingkan dengan email non-spam.

Mari kita bayangkan ada banyak email yang sudah kita labeli sebagai spam atau bukan. Kita bisa menghitung P(spam), yaitu probabilitas suatu email adalah dikategorikan sebagai spam, dan P(gratis∣spam), yaitu probabilitas kata "gratis" muncul dalam email spam. Begitu juga kita bisa menghitung P(non−spam) dan P(gratis∣non−spam). Dengan berdasarkan data ini, kita bisa menghitung apakah email baru dengan kata "gratis" kemungkinan besar adalah spam atau bukan.

Proses ini menjadi dasar dari banyak aplikasi Naive Bayes lainnya, seperti filter spam di email, prediksi cuaca, dan diagnosis medis. Untuk memahami lebih dalam bagaimana persamaan matematika ini bekerja dalam proses perhitungannya, mari kita lanjut ke poin berikutnya!

Bagaimana cara kerjanya? Sebagai contoh, jika kita memiliki 1000 email, di mana 500 adalah spam dan 500 sisanya adalah non-spam. Dari 500 email spam, 100 diantaranya mengandung kata "gratis", sedangkan dari 500 email non-spam, hanya ditemukan 10 yang mengandung kata "gratis". Berdasarkan itu, kita bisa menghitung dengan cara berikut:

P(spam)=500/100=0.5 P(non-spam)=500/100=0.5 P(gratis|spam)=100/500=0.2 P(gratis|non-spam)=10/500=0.02

Dengan pemanfaatan Teorema Bayes, kita dapat melakukan proses perhitungan terhadap P(spam∣gratis) dengan sebagai berikut: P(spam|gratis)=P(gratis|spam).P(spam)P(gratis) Untuk menghitung P(gratis), kita gunakan:

P(gratis)=P(gratis|spam).P(spam)+P(gratis|non-spam).P(non-spam) P(gratis)=(0.2 . 0.5)+(0.02 . 0.5) = 0.11 Akhirnya, kita bisa menghitung P(spam∣gratis): P(spam|gratis)=0.2 . 0.50.11=0.91

Jadi, probabilitas bahwa email dengan kata "gratis" adalah spam sekitar 91%. Bagaimana, mudah untuk dipahami bukan? Naive Bayes dapat diimplementasikan dalam kehidupan sehari-hari loh yang dibahas pada poin selanjutnya!